Concrete-Pictorial-Abstract Instruction

The Borenson Math products, whether related to algebra or fractions, employ the C-P-A mode of instruction. This method is also referred to as C-R-A, standing for Concrete-Representational-Abstract.  Jerome Bruner, in his seminal work Toward a Theory of Instruction (Bruner, 1976), suggested that the concrete experience could serve as a foundation for the pictorial and abstract modalities. It would provide the student for something “to fall back on” should they forget the procedures when working at the abstract stage.

Below we illustrate the C-P-A instructional approach as employed in Level I of Hands-On Equations. These concrete and pictorial methods may be used as early as the 3rd and 4th grades with regular students and the 5th grade with students having mild learning disabilities. The mental and abstract written solutions may be used as early as the 5th grade with regular students, and the 6th grade with students having mild learning disabilities.

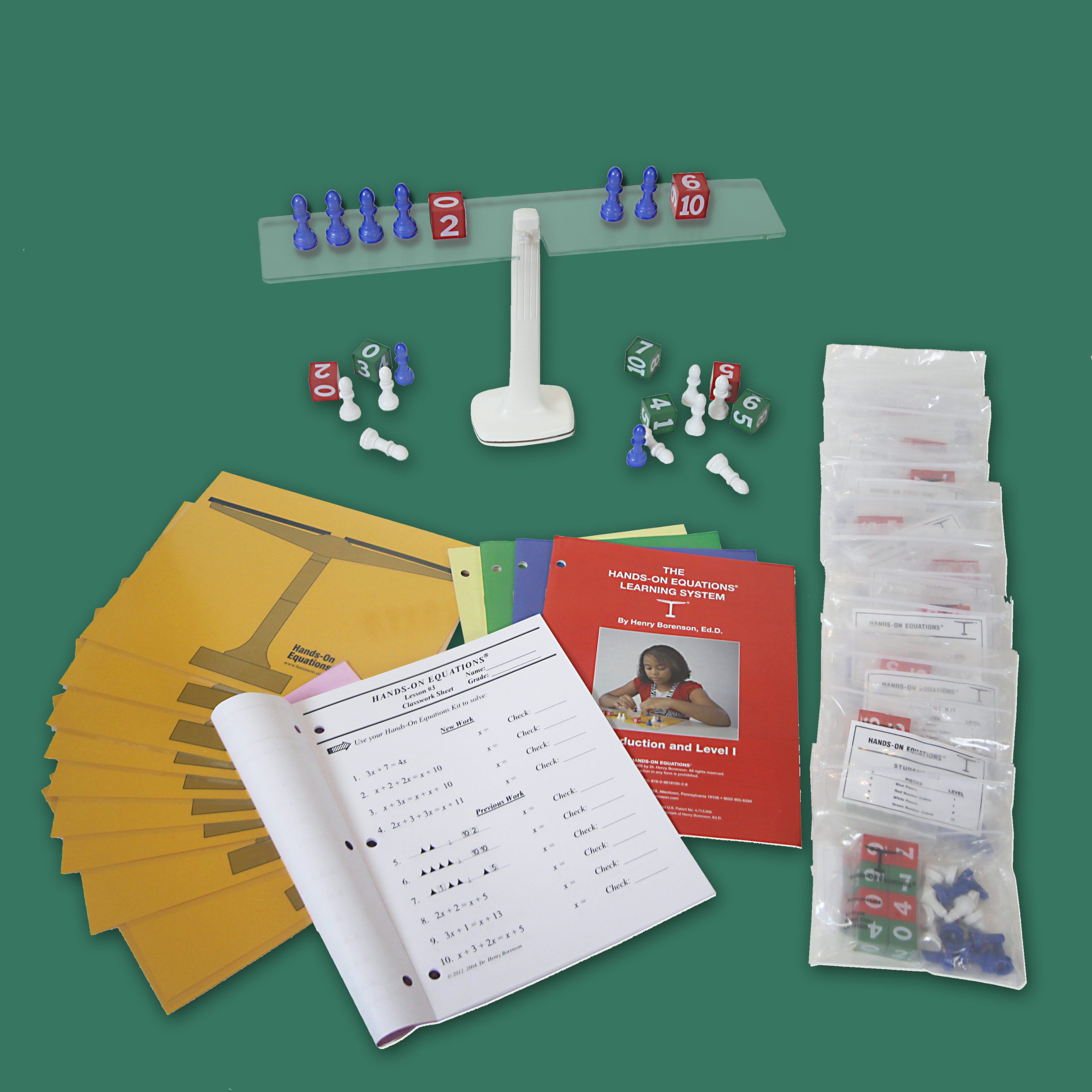
Figure 1. Class set of Hands-On Equations.

Hands-On Equations Concrete Solution

We illustrate the process with an equations taken from Lesson 4 of the program. Figure 2 shows the Hands-On Equations representation for the equation 4x + 5 = 2x + 13. In this representation, the unknown x is represented by a blue pawn. Since, by definition, 4x = x + x + x + x , we designate 4x by the value of the four pawns. The constants are represented by numbered cubes. The game pieces are assembled on an image of a balance scale, with the two sides of the equation displayed on the two sides of the balance scale. The value of the game pieces on each side of the balance are additive, since weights on a balance scale are additive.The understanding is that the total weight or value of the pieces on either side of the balance is the same.

Figure 2. Hands-On Equations concrete representation of the equation 4x + 5 = 2x + 13.

Figure 3 shows the solution to the same equation on the Teacher Demonstration Scale. The student performs “legal moves” to simplify the equation. Removing two blue pawns from each side of the balance scale, and a value of 5 from the number cubes, the student is left with two pawns having a value of 8. The student  concludes that each pawn, or x,  has the value of 4. To do the check, the student resets the original physical setup shown in Figure 2, substitutes the value of 4 for x, and sums each side to get a check value of 21. The student writes the answer as x = 4, Check: 21 = 21.

Figure 3. Concrete solution of 4x + 5 = 2x + 13 demonstrated on the Teacher Demonstration Scale.

Hands-On Equations Pictorial Solution

Lesson 7 introduces students to the pictorial solution. As illustrated in Figure 4, students draw a picture of the balance scale. The unknown is represented by a shaded triangle, and the number constants are represented by boxed numbers. The legal move of removing pawns is shown using arrows; the legal move with the cubes is shown by cross-out and replacement. The check is done in the original pictorial representation, redrawn if necessary.

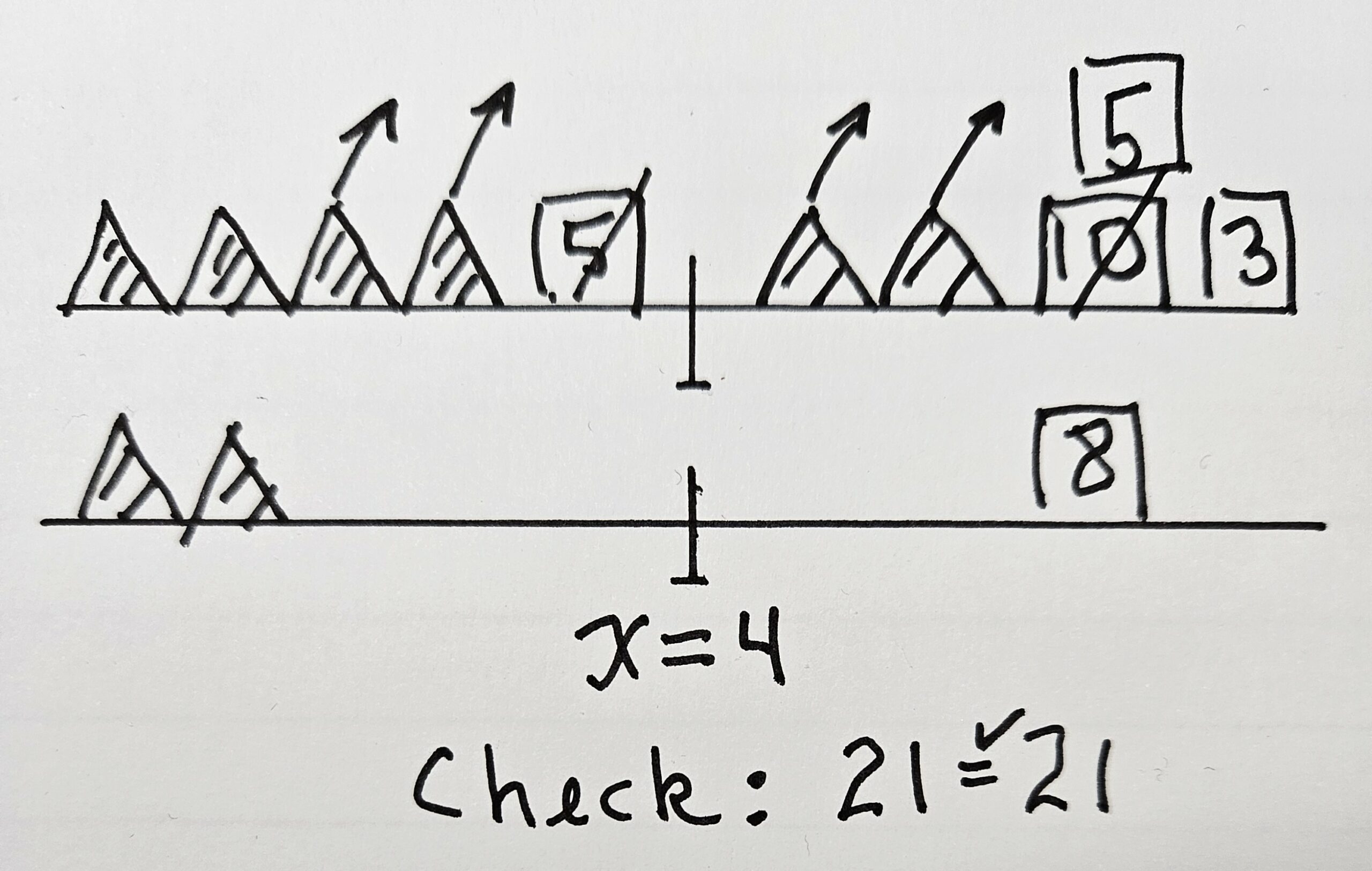
Figure 4. Hands-On Equations pictorial solution for 4x + 5 = 2x + 13.

Hands-On Equations Abstract Solution

Mental solution. In the mental solution, looking only at the equation, students visualize the game pieces on the balance scale. They mentally remove two blue pawns and a 5-cube value from each side. They now mentally see two blue pawns on one side, and cube(s) having a value of 8 on the other. Since two blue pawns have the value of 8, each one has the value of 4. The check is done in the original equation. On the left side, we have 4 times 4, plus 5, which are 21. On the right side, we have 2 times 4, plus 13, which are also 21. This approach has been presented in our workshops and is presented in our webinars.

Abstract Written Solution. Optional Lesson 26 enables the teacher to introduce students to the abstract written notation. It is optional since for students in Grades 3 and 4 the objective is only the concrete and pictorial solutions. The written solution for our equation is illustrated in Figure 6. Just as students remove two pawns, or 2x’s, from each side of the concrete and pictorial notation, they do the same in the abstract solution. Hence, the transfer is direct. Notice that the equal sign is copied at each step to be sure that the same procedure is being performed on both sides of the equal sign.

Figure 5. Students mentally solve the equation as they  visualize the action on the game pieces.

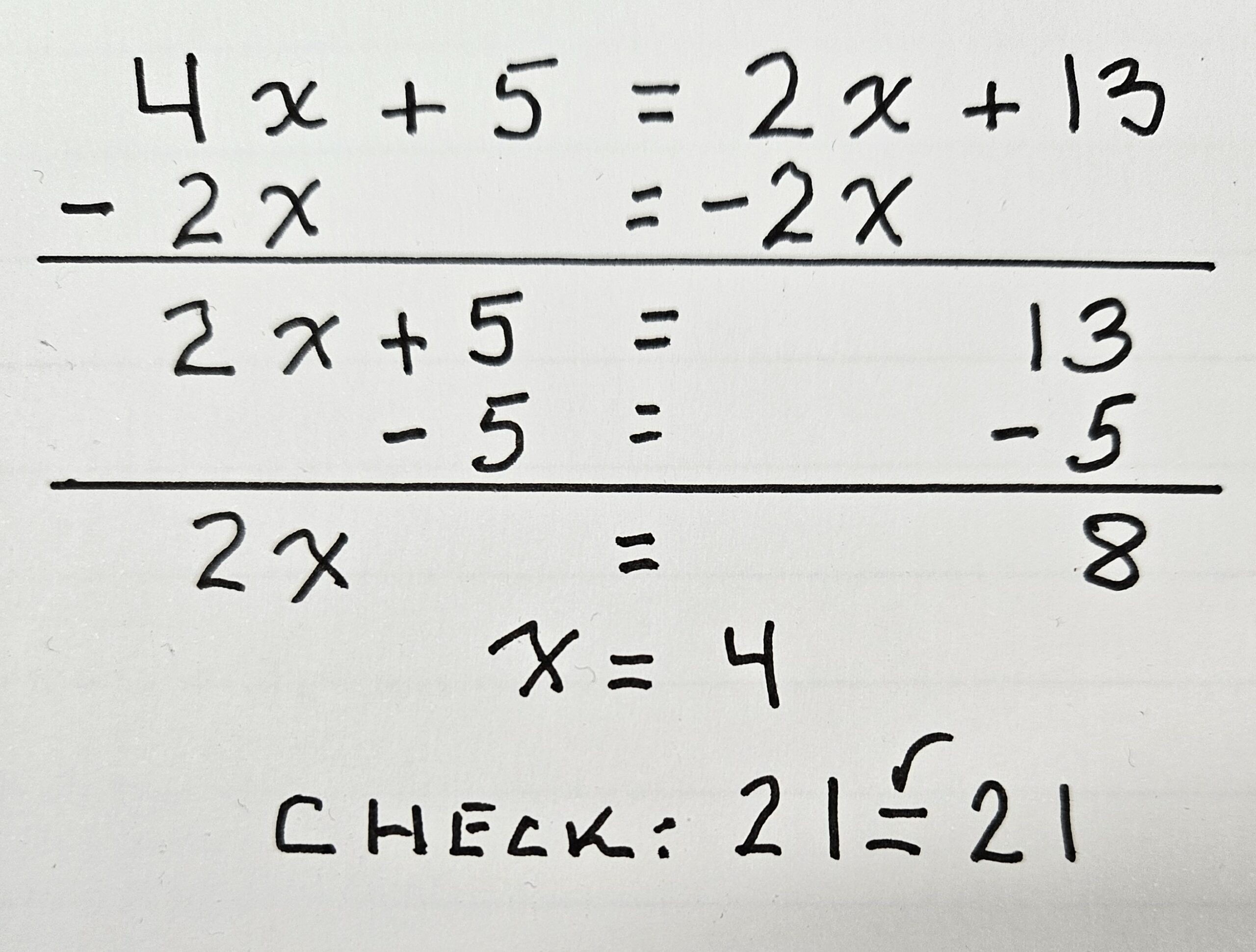
Figure 6. Written abstract solution of 4x + 5 = 2x + 13.